Building a zkSNARK Application with Keelung: Merkle tree membership

This is not a tutorial, but rather an overview of how to build a zkSNARK application from scratch with Keelung. Some steps may be skipped or simplified. Please refer to other parts of the documentation if you are unable to reproduce the process exactly.

Introduction

Zero-knowledge proofs enable one party to prove the validity of a statement to another party without revealing additional information. zkSNARKs are a popular implementation of zero-knowledge proofs due to their efficiency and privacy.

In a basic zkSNARK setup, there is a public problem statement that describes what needs to be proven. Two parties are involved, a prover and a verifier. The prover provides a witness of the statement being true, while the setup processes the witness into a proof which validates the statement. The setup allows the verifier to check for the validity of the statement only with the proof provided. As required by zkSNARKs, the proof is succinct and non-interactive, meaning it allows the verifier to verify the statement’s validity without any additional information or interactions.

In this blog post, we will show how to build an example of zkSNARKs applications through a series of steps. We at BTQ are introducing Keelung, the domain-specific language (DSL) we are building in Haskell to describe the public statements (in the form of zkSNARK circuits). Our compiler produces constraints from the circuits, which are then used to generate and verify a proof with the Aurora protocol.

Keelung offers a streamlined interface for interacting with its compiler, prover, and verifier, so that you don't have to go digging through their code.

If you want to try it out on your machine, please read the documentation on how to install Haskell and compile Keelung programs.

Example: Merkle tree membership

Imagine a scenario: we have a root hash of a Merkle tree that represents a public group, and there is a member of this tree who possesses a leaf hash of the tree. They can easily prove that they are part of the tree by showing the hash and the path (all the nodes and their siblings along the path from the leaf to the root), and anyone can verify this by hashing these nodes together.

As described above, it is clear that in order for anyone to verify a hash, one must reveal the leaf hash. This could be a downside for private membership, where people don’t wnat to reveal their identity. This is where zero-knowledge proofs and zkSNARKs come in to play.

Let's list all the information needed and their requirements in this scenario:

A public statement of one hash belonging to a Merkle tree where the root hash is public.
A member who possesses a leaf hash that is a member of the tree and can generate a proof of its existence without revealing its content.
A third party that wants to verify the proof.

To generate a zero-knowledge proof from private information (in this case, the leaf hash and the path), a member requires a prover program. To verify the proof, anyone can use a verifier program that takes the proof and the public statement, and outputs whether or not it satisfies the statement.

Describing the problem with Keelung

Luckily, we have all the tools we need to make the magic happens. We can write a Keelung program that describes the statement:

module MerkleTree where

import Data.Foldable (foldlM)
import Hash.Poseidon
import Keelung

getMerkleProof :: Int -> Comp Field
getMerkleProof depth = do
  leaf     <- inputField Private
  siblings <- inputList2 Private depth 2
  indices  <- inputList Private depth :: Comp [Field]
  foldlM
    (\_digest (_i, p) -> hash p)
    leaf
    (zip indices siblings)

You can skip this part if details do not interest you.

Let's take a quick look at getMerkleProof. Keelung is a DSL defined in Haskell, meaning that a Keelung program is essentially a Haskell program. The Comp monad defines all the operations in Keelung. If you're not familiar with what a monad is, just remember that "Keelung programs" refers to programs of type Comp X, where X is the type of the output of a circuit. Within Comp, you can invoke other Keelung operations of type Comp Y, such as declaring input fields.

The function getMerkleProof requires an integer argument depth, which specifies the depth of the Merkle tree. This function generates constraints on trees of the specified depth.

The input functions described variables that are inputs to the circuit. The first variable leaf is an input field which will represent the leaf node that we want to prove the existence of. The second variable siblings is a list of 2-element lists (inputList2 specifies the input list to be 2-dimentional) which contains the siblings of the nodes on the path from the leaf node to the root of the Merkle tree. The third variable indices is a list of indices that represent the path from the leaf node to the root, such that the siblings[0][indices[0]] is the leaf we have.

Notably, there are private and public inputs, the difference is that private inputs will later be hidden in the zkSNARK proof, while public inputs will not.

foldlM is a common Haskell function, it takes a binary function and an initial value and then applies the function to each element of a list in turn. In this case, the binary function is a hash function which takes a pair of an index and a sibling and produces a new digest. The foldlM function starts with the leaf node and applies the hash function to each of the siblings in siblings and their corresponding indices in indices, resulting in a new digest.

The final result is the digest produced by the foldlM function, which represents the root of the Merkle tree. The digest is returned as the result of the getMerkleProof function in the Keelung monad Comp wrapped in a Field type.

Generating constraints from Keelung programs

The above example of Merkle tree membership can be found in our examples repository. We can load this program into Haskell REPL using the building tool Stack, and call the compile function defined in the Keelung library to generate constraints:

$ stack repl
> :l MerkleTree.hs
> compile GF181 (getMerkleProof 2)

The REPL should display the constraints of all variables in this program, along with whether they are public or private.

      ...
      ...
      $5395 * $5398 = $5394
      $5396 * $5397 = $5395

  Variables (5401):

    Output variable : $0
    Private Input variables: $1 ... $7

}

The size of the constraints is usually too large to be human-readable. However, this is not a problem, as R1CS is designed for proving systems to generate and verify proofs. We will only print the constraints directly when debugging.

Generating and verifying proofs

Our exceptional coworkers have developed a prover and verifier based on the Aurora protocol with libiop. The prover, aurora_prove, takes a set of constraints (e.g., R1CS generated from Keelung programs), private and public inputs, and generates a zkSNARK proof. The verifier, aurora_verify, takes the same set of constraints, public inputs, and a proof generated by the prover, then outputs whether the constraints are satisfied.

Although it is possible to interact with the prover and verifier directly after installation, the Keelung library has built-in support for communicating with these binaries. This enables the generation and verification of proofs to be carried out from the REPL.

The generate function in Keelung is used to generate and validate R1CS. generateDefault do the same thing with default file paths. Below is an example of its usage:

> generateDefault gf181 (getMerkleProof 2) [] [12,12,13,-339407639512599616321326372666980567874739108165133258,-735671215241697176388195510059578733309042544167985940,1,1]

The first argument is the field for computation. The second argument is a computation of type Comp X that describes the R1CS to be generated, in this case getMerkleProof 2. The third argument is a list of public inputs and the fourth argument is a list of private inputs.

Multiple files will be generated after calling generate. The parameter.json file contains fixed parameters for both provers and verifiers, while circuit.jsonl is the representation of the generated constraints in R1CS. The witness.jsonl contains assignments to all the public and private variables. After generating these files, the prover is actually invoked, and a proof file is generated in the directory. generate also produces a file inputs.jsonl, which is identical to witness.jsonl but only contains the public part of the variables.

Verification of the proof is done using the verifyDefault function in the library. This function calls the verifier with the parameter.json, circuit.jsonl, inputs.jsonl, and proof files (verify, on the other hand, lets you specify the file paths).

> verifyDefault

If generateDefault ran successfully, verifyDefault should display the verifier's messages, including whether the constraints are satisfied given the public inputs and the proof.

(enter) Aurora SNARK verifier
...
* Verifier satisfied: true

Summary & Conclusion

In this blog post, we have provided an introduction to zero-knowledge proofs and zkSNARKs, cryptographic tools that allow for secure communication without revealing additional information. We have demonstrated their applications by presenting an example of proving membership in a Merkle tree, using the Keelung domain-specific language to describe the problem, generating constraints from the circuits, and using a prover and a verifier to generate and verify proofs.

Let’s revisit how the process might work in real life:

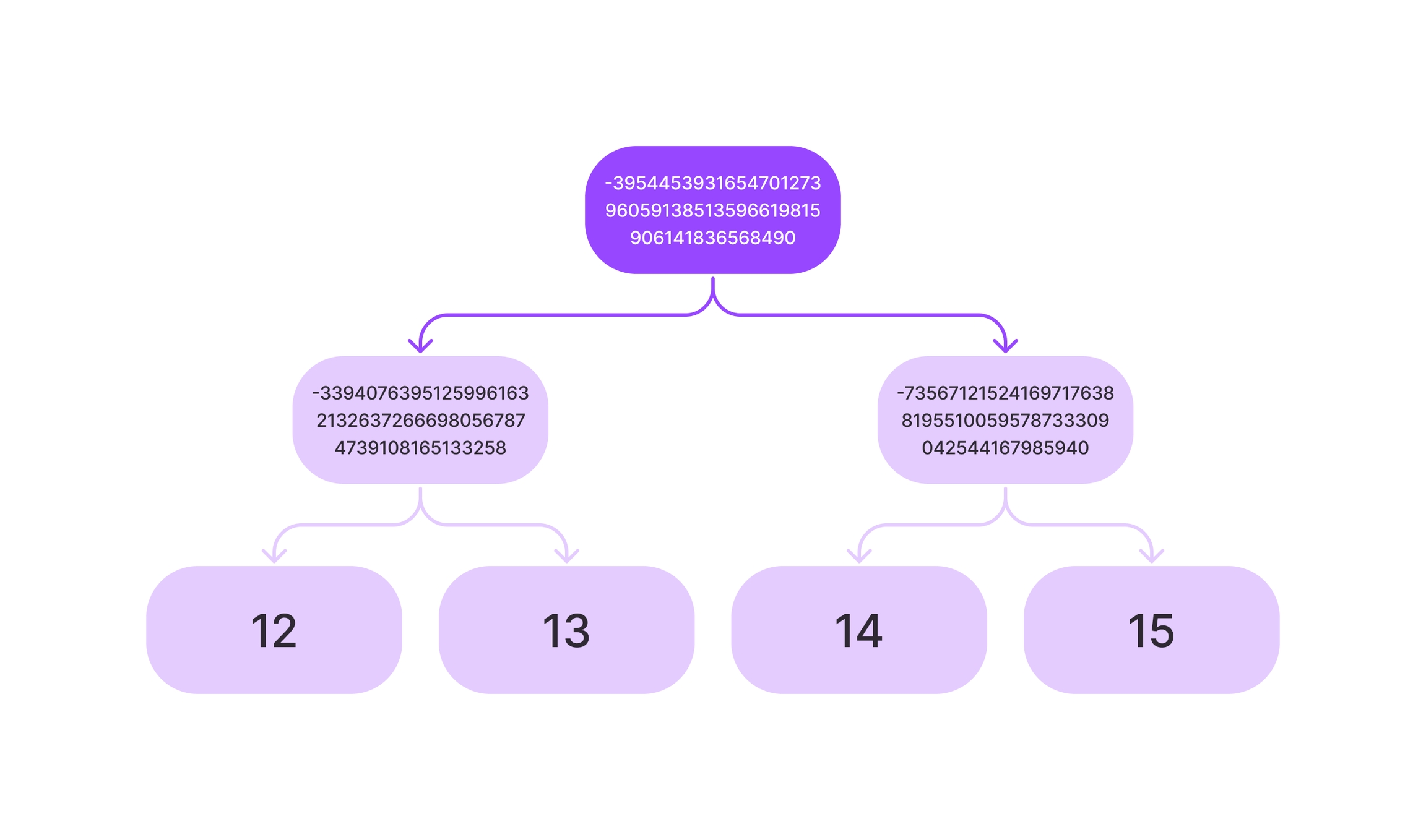
There exists a public information of a Merkle tree that is the hash of it’s root, say -395445393165470127396059138513596619815906141836568490
From the all-knowing perspective, we know that the tree is constructed from four members: 12, 13, 14, and 15. The Poseidon hash function, provided by the Keelung standard library, is used to generate hashes given any two numbers.
Due to the nature of hashing, the public does not know which members are actually in the Merkle tree.
If a party has a member of the Merkle tree, such as 12, they can make it public along with its adjacent node, the path to its root, and the nodes adjacent along the path. In this case, 13, -339407639512599616321326372666980567874739108165133258, and -735671215241697176388195510059578733309042544167985940 are provided.
Anyone can hash 12 and 13 and check it is -339407639512599616321326372666980567874739108165133258, then hash it with -735671215241697176388195510059578733309042544167985940 to find out the result is indeed the public root hash.
But in this way, the party must reveal that the number they possess is 12. That’s where zkSNARKs can help if private membership is needed.
Instead of revealing the nodes, the public hash of the Merkle tree and a circuit.jsonl generated from our Keelung pogram that describes the problem are made public from the beginning.
The party that wish to prove their membership takes the public description and generates a zkSNARK proof with their private info, in this case the 12 they possess and the path from it to the root hash.
Other parties no longer needs the private info itself to verify the membership, now they takes the public circuit.jsonl and the zkSNARK proof provided by the prover, and verify it with the verifier we provided.

This example shows the power and potential of zero-knowledge proofs and zkSNARKs, and how Keelung plays a crucial part in the process. There have and will be more usage in various applications, including privacy-preserving transactions, voting systems, and more. We hope this post serves as a useful resource for those interested in understanding and implementing zkSNARK projects.