Poseidon Hash Function

Introduction

Poseidon is a cryptographic hash function designed specifically for use in zero-knowledge proof systems, such as R1CS and PLONK. It offers improved performance compared to other existing hash functions, by a factor of up to 40 times. The function uses a substitution-permutation network design, a well-known design in symmetric cryptography, and supports varying finite field sizes, making it a versatile option for a variety of zero-knowledge proof applications.

About this tutorial

In this tutorial, our goal is to demonstrate the implementation of Poseidon in Keelung. We will showcase how to use fold, a commonly used method in functional programming, to repeatedly apply an action on the state and produce the desired result.

Here's the link to the code of Poseidon in Keelung.

Overview

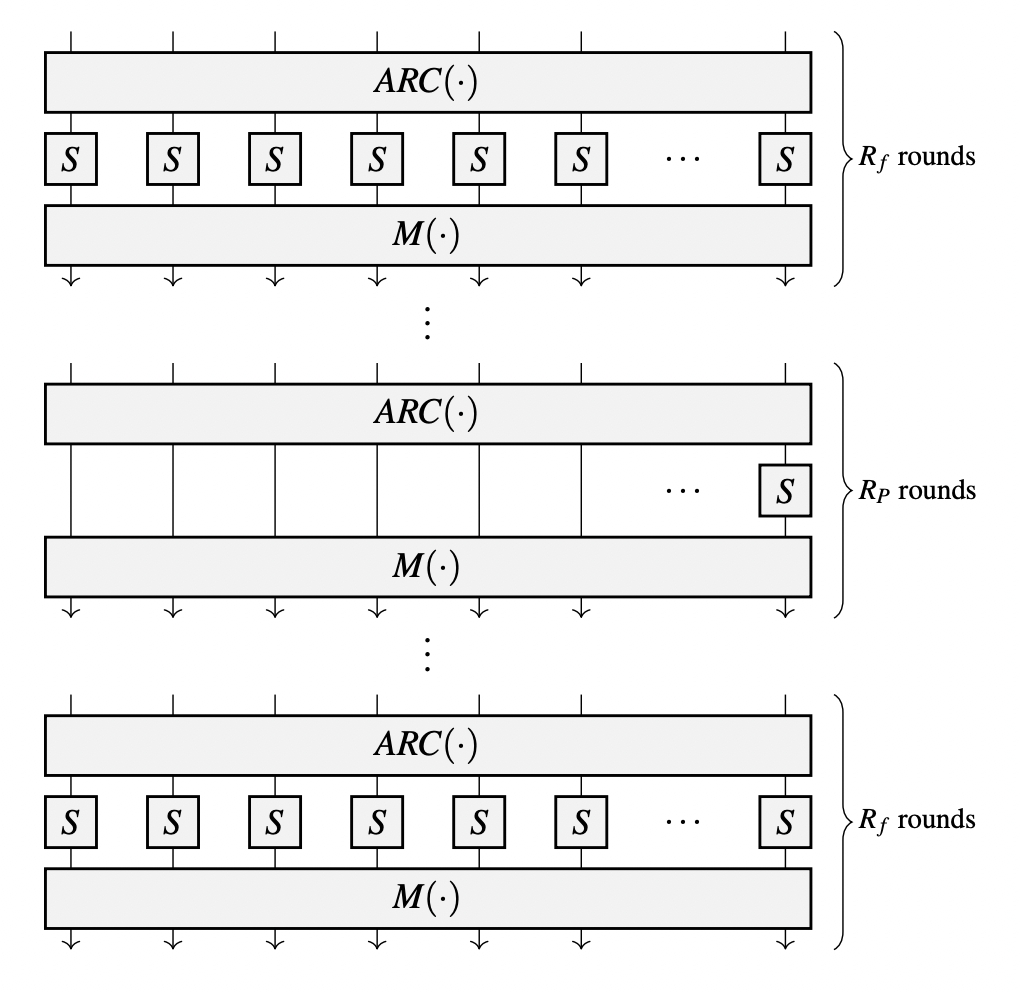
Poseidon is structured as a sequence of rounds, each of which applies substitution and permutation operations on the input data.

Multiple Iterations of the "Round Function": building block of Poseidon permutation

Round

As shown in the diagram above, each round consists of three components. Suppose that we have defined Haskell functions for each of these components:

• arc for ARC

• sbox for S

• mix for M

We can defined the round function as the composition of these components. It takes [Field] as input and returns [Field] as output:

round :: [Field] -> [Field]
round = mix . sbox . arc

Because sbox and arc both actually takes the current round number as input, let's generalize round a bit:

round :: Int -> [Field] -> [Field]
round r = mix . sbox r . arc r

Apply round multiple times

Suppose we have to apply the round function 3 times on an input data initState, each time with the current round number. The resulting output would be expressed as:

round 2 (round 1 (round 0 initState))

We can construct this expression using the foldl function:

foldl (\state r -> round r state) initState [0, 1, 2]

Let's evaluate the expression above step by step, and see how it actually works:

foldl (\state r -> round r state) initState [0, 1, 2]
    =>
foldl (\state r -> round r state) (round 0 initState) [1, 2]
    =>
foldl (\state r -> round r state) (round 1 (round 0 initState)) [2]
    =>
round 2 (round 1 (round 0 initState))

If you want to know more about fold, here's a simple article explaining how it works under the hood.

Components

Here's a detailed walk through of all components in the actual implementation of Poseidon.

Main function hash

hash :: [Field] -> Comp Field

Let's look at the main function hash first. It takes as input a message msg, represented as a list of Field values, and returns a Field as the hashed result.

The function performs the following steps:

1. check if the message length is valid (i.e., not null and less than or equal to 6).

hash msg = do
  when
    (null msg || length msg > 6)
    (error "Invalid message length")

2. initialize constants t, roundsP, f, p, c, and m.

  let t = length msg + 1
  let roundsP = [56, 57, 56, 60, 60, 63, 64, 63]
  let f = 8
  let p = roundsP !! (t - 2)
  let c = Constant.c ! (t - 2)
  let m = Constant.m ! (t - 2)

3. Initialize the state with 0 as the first element and the message as the rest.

  let initState = 0 : msg

4. Define the round function, which consists of three components:

   1. "AddRoundConstants" as arc

   2. "SubWords" as sbox

   3. "MixLayer" as mix

  let round r = mix m . sbox f p r . arc c (r * t)

5. Use foldlM to apply the round function p times on the initial state.

  result <- foldlM (\state r -> reuse (round r state)) initState [0 .. f + p - 1]

6. Finally, return the first element of the final state as the hash value.

  return $ head result

AddRoundConstants arc

The arc function implements the "AddRoundConstants" component of the round function.

arc :: Vector Field -> Int -> [Field] -> [Field]
arc c it state = mapI (\i x -> x + c ! (it + i)) state

The arc function takes 3 inputs:

• A Vector Field of constants named c.

• An integer it for selecting constants in c.

• A list of Field named state.

It returns a new list of Field by adding c ! (it + i) to each element x of the input list state at index i, using the mapI function.

SubWords sbox

sbox :: Int -> Int -> Int -> [Field] -> [Field]
sbox f p r state = mapI go state
  where
    go 0 x = fullSBox
    go _ x = if r < f `div` 2 || r >= f `div` 2 + p then fullSBox x else x
    -- Full S-box of x⁵
    fullSBox x = x * x * x * x * x

fullSBox takes an element x from the state list and computes x⁵ as output.

Depending on the round number r and other parameters like p and r, sbox applies fullSBox on each element x of the state list.

MixLater mix

mix :: Vector (Vector Field) -> [Field] -> [Field]
mix m state =
    map
      (\i -> sum (mapI (\j x -> x * (m ! i ! j)) state))
      [0 .. length state - 1]

It takes two inputs, a matrix m of field elements, and a state represented as a list of field elements. The function calculates the dot product of each row of the matrix with the state and returns the result as a new list of field elements.

The calculation is performed using the map and sum functions. The map function maps each element of the state to its dot product with a row of the matrix. The sum function takes the sum of these dot products to obtain the final result.

The length of the resulting list is equal to the number of rows in the matrix, which is equivalent to the length of the state.